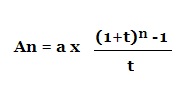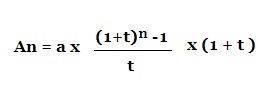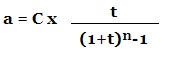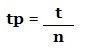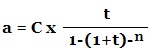Calculs financiers

1) Les intérêts composés

a) La valeur acquise

La valeur acquise est la somme du capital initial et des intérêts générés au terme d’un certain nombre d’années de placement.

Calcul de la valeur acquise : A = C x (1+t)ⁿ

A = Valeur acquise à intérêts composés

C = Capital

t= taux d’intérêt

n = nombre de périodes

exemple : Vous placez votre un capital de 10 000 € à la banque pendant trois ans au taux annuel de 4%.

Combien obtiendrez vous dans 3 ans ?

A = 10 000 x (1,04)³ = 11 248,64 €

b) Le calcul de la valeur acquise d’une suite d’annuités

Il est également possible de calculer la valeur acquise d’une suite d’annuités égales. L’annuité est un versement ajouté chaque année destinée à constituer un capital. Selon la date d’ajout de l’annuité au capital, le calcul de valeur acquise varie :

calcul de versements effectués en fin de période :

an = somme des annuités versées + intérêts générés

a= annuité (versement effectué en fin de période)

t = taux d’intérêt

n = nombre de périodes

exemple :Vous placez 1 000 € par an en fin d’année au taux de 5 % pendant 8 ans. Combien aurez vous au bout de ces 8 ans ?

1 000 x (1,05^8 -1/0,05) = 9 549,11 €

Pour trouver la valeur acquise avec les versements en début d’année,

utilisez le calcul suivant :

exemple : Vous placé 1 000 € par an au taux de 5% pendant 8 ans, mais cette fois en début d’année. Combien aurez vous dans 8 ans ?

9 549,11 x (1+0,05) = 10 026,57 €

c) La valeur actuelle

La valeur actuelle est la valeur aujourd’hui d’une somme disponible dans le futur.

Calcul de la valeur actuelle :

V = C x (1+t)-ⁿ

V = valeur actuelle

C = capital

ⁿ = période

t = taux

exemple : un client d’une banque souhaite obtenir la somme de 140 000 € le 31 décembre 2019.

Quelle somme doit-il placer le 1er janvier 2014 avec un taux d’intérêt de 6 % ?

V = 140 000 x (1+0,06)-⁶ = 98 694,48 €

d) La valeur actuelle d’une suite d’annuités de placement

On peut également calculer la valeur actuelle d’une suite d’annuités.

Calcul de la valeur d’une suite d’annuités :

a = valeur actuelle d’une suite d’annuités en fin de période

c = capital

ⁿ = période

t = taux

exemple : un client d’une banque souhaite réunir la somme de 20 000 € dans 5 ans sur un compte à 6 % de taux d’intérêts. Quel somme doit-il placer chaque année ?

20 000 x (0,06/((1+0,06)⁵-1) = 3 547,98 €

e) Le taux proportionnel et le taux équivalent

La plupart du temps, les intérêts d’une banque sont en année. Cependant, si les intérêts sont calculés en moins d’une année (semestre, mois) ou plus d’une année, le calcul change.

Le taux proportionnel est utilisé lorsque les intérêts sont calculé de façon inférieur à une année. Le calcul consiste à diviser le taux annuel d’intérêt par le nombre de période dans l’année.

Calcul du taux proportionnel :

exemple : Si un livret propose 4% par an d’intérêt, le taux proportionnel sera de 0,33% par mois (4 % par an /12 mois).

Le taux équivalent est le taux d’intérêt sur une durée supérieur à un an. Dans ce cas, il faut tenir compte des intérêts composés.

Calcul du taux équivalent :

exemple : si vous avez 5 000 € placé sur un compte pendant 2 ans au taux annuel de 4,5%, quel sera le taux équivalent mensuel ?

12 $surd$ (1+0,045) -1= 0,0036748

2) Le remboursement des emprunts

a) Le remboursement des emprunts par amortissements constants

L’emprunteur rembourse son prêt à l’organisme prêteur en annuités de remboursement. Il doit rembourser le capital emprunté plus les intérêts. La somme qui est remboursé chaque année se nomme amortissement.

Calcul de l’annuité : annuité = intérêts + amortissement

Le remboursement par amortissements constants consiste à rendre chaque année un même montant du capital emprunté.

Amortissement constant = montant de l’emprunt / durée de remboursement

les intérêts sont calculés chaque année sur le capital restant à rembourser.

Le capital restant dû au début de l’année N est égal au capital de l’année précédente auquel on soustrait l’amortissement de l’année.

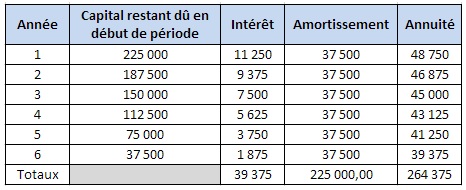
exemple : Vous avez besoin de 225 000 €, vous souhaitez emprunter sur 6 ans avec un taux d’intérêt de 5 %.

Calcul de l’amortissement : 225 000 / 6 = 37 500

Calcul des intérêts de la première annuité : 225 000 x 0,05 = 11 250

Voici le tableau d’amortissement pour un prêt de 225 00 € sur 6 ans au taux d’intérêt de 5% :

Le coût du crédit est de 39 375 € et le coût d’acquisition du bien est 264 375 €.

b) Le remboursement des emprunts par annuités constantes

Dans ce cas, les annuités sont constantes.

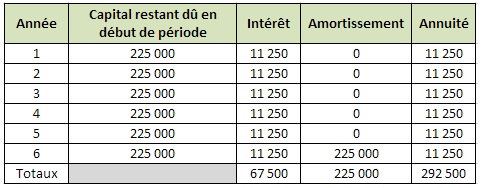
Calcul de l’annuité de remboursement :

C = montant de l’emprunt

t = taux d’intérêt

n = nombre de période

exemple : avec le même exemple, vous voulez un prêt à 225 000 € sur 6 ans au taux annuel de 5 % avec des annuités constantes cette fois.

calcul de l’annuité : 225 000 x (0,05/(1-(1,05)^-6)) = 44 328,93

Le tableau d’amortissement sera ainsi :

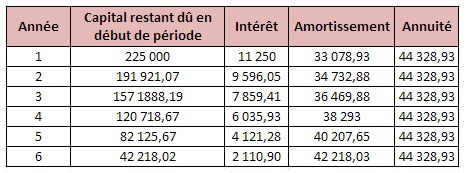
C) Les emprunts « in fine » ou non amortissables

Il s’agit de prêts dont le capital est entièrement remboursé à la fin de la dernière échéance.

exemple : vous souhaitez louer une maison sur 6 ans d’une valeur de 225 000 €, puis l’acheter à la fin de votre période de location. Le taux d’intérêt est de 5 %.